| Переглянути всі підручники | |||||||||||||
| << | < | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | > | >> |
|
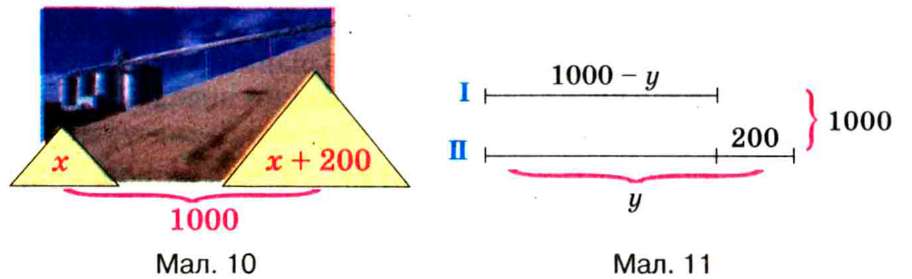
Часто у складанні рівняння допомагає малюнок або схема (мал. 10). |
 |
Дану задачу можна розв'язати й іншими способами.
Якщо на другому току є у т зерна, то на першому (1000 - у) т (мал. 11). Оскільки на другому току зерна на 200 т більше, то 1000 -у+ 200 = у, звідси у = 600, 1000 - у = 400.
Відповідь така сама.
Малюнок 10, малюнок 11, рівняння 1000 - у + 200 = у — це три різні математичні моделі прикладної задачі 1. В математиці прикладними називають задачі, умови яких містять нематематичні поняття.
Модель завжди подібна до оригіналу. У ній відображаються ті чи інші важливі властивості досліджуваного об'єкта. Такими є зменшені моделі автомобіля, літака, будинка. Глобус — модель Землі, лялька — модель людини. Якщо модель побудовано на основі рівнянь, формул чи інших математичних понять, її називають математичною моделлю.
Для розв'язування задач на рух також використовують різні моделі. Бажано пам'ятати, що при рівномірному русі пройдена тілом відстань дорівнює добутку швидкості на час (s = vt). При цьому всі значення величин слід виражати у відповідних одиницях вимірювання. Наприклад, якщо час дано в годинах, а відстань — у кілометрах, то швидкість треба виражати в кілометрах за годину. Якщо тіло рухається при наявності течії, то його швидкість руху за течією (проти течії) дорівнює сумі (різниці) його власної швидкості і швидкості течії. За допомогою схем багато задач на рух можна розв'язати усно (№ 124). Деякі складні задачі вимагають для розв'язування побудови кількох моделей.
Розглянемо задачу, скласти рівняння до якої допомагає таблиця — ще один вид математичних моделей.
| Переглянути всі підручники | |||||||||||||
| << | < | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | > | >> |